To find a shortest path in a weighted graph a well known
Dijkstra’s algorithm can be used [1].
Let us implement it in C++ as an exercise.
To start - we will have an Edge structure for our fixed
size graph and we will store edges in an array.
struct Edge
{
int to;
int weight;
};
template<int VertexCount>
struct Graph
{
public:
std::array<std::vector<Edge>, VertexCount> AdjList;
void AddEdge(int from, int to, int weight)
{
--from; --to; // 0 indexed
assert(from >= 0 && from < VertexCount);
assert(to >= 0 && to < VertexCount);
AdjList[from].emplace_back(to, weight);
AdjList[to].emplace_back(from, weight);
}
};In this implementation we cannot add more vertices, but can
dynamically add edges.
Edges are numbered from 1 to VertexCount, but indexed from 0 to
VertexCount in the internal array.
The function implementing the Dijkstra’s algorithm will accept a Graph and the source vertex as an input and will return an array holding the shortest path to each vertex.
template<int VertexCount>
std::array<int, VertexCount> FindShortestPaths(Graph<VertexCount>& graph, int sourceVertex);Let us also have a helper function to print the shortest paths.
template<std::size_t VertexCount>
void printPaths(int source, const std::array<int, VertexCount>& paths)
{
std::cout << "Shortest paths:\n";
for (auto i = 0; i < paths.size(); ++i)
{
if (paths[i] < std::numeric_limits<int>::max())
std::cout << std::format("{}->{} = {}\n", source, i + 1, paths[i]);
}
}Then we can construct a graph and find the shortest path from the first vertex as an example.
int main()
{
Graph<6> graph;
graph.AddEdge(1, 2, 7);
graph.AddEdge(1, 6, 14);
graph.AddEdge(1, 3, 9);
graph.AddEdge(2, 3, 10);
graph.AddEdge(2, 4, 15);
graph.AddEdge(3, 6, 2);
graph.AddEdge(3, 4, 11);
graph.AddEdge(4, 5, 6);
graph.AddEdge(5, 6, 9);
constexpr int from = 1;
auto shortestPaths = FindShortestPaths(graph, from);
printPaths(from, shortestPaths);
return 0;
}The constructed graph can be visualised as follows.

With this out of the way, let us write the algorithm itself.
Once we checked that the supplied vertex is valid we can fill the result array of shortest paths with a sentinel value, indicating that the distance is unknown. We chose a max integer for this.
We also know that distance to the vertex itself is zero.
/*... */ FindShortestPaths(Graph<VertexCount>& graph, int sourceVertex)
{
--sourceVertex; //0 indexed
assert(sourceVertex >= 0 && sourceVertex < VertexCount);
std::array<int, VertexCount> shortestPaths;
shortestPaths.fill(std::numeric_limits<int>::max()); // distance to all vertices is unknown
shortestPaths[sourceVertex] = 0; // path to the source vertex itself it zero
//...
}To make sure that we relax the shortest edges first we use a minimum
heap data structure [2], which in C++ is represented
with a priority_queue. In the heap, we store (vertex,
distance) pairs, where distance - is the total distance to reach this
vertex so far.
In order to compare the edges a custom comparator is needed.
We initially fill the heap with all the Paths adjacent to the source
vertex.
struct Path
{
int to;
int distance;
};
/*... */ FindShortestPaths(Graph<VertexCount>& graph, int sourceVertex)
{
//...
auto comparator = [](const Path& left, const Path& right)
{
return left.distance > right.distance;
};
std::priority_queue<Path, std::vector<Path>, decltype(comparator)> minHeap;
minHeap.emplace(sourceVertex, 0); // start at the source vertex
//...
}Now the core of the algorithm - we pop the closest edge from the heap. If the new path to the vertex this edge is going to is shorter than what we know so far - we update the shortest path to the target vertex.
Then we add all edges connected to the target vertex into the heap.
The algorithm keeps running until all the vertices are visited (i.e. the heap is exhausted).
/*... */ FindShortestPaths(Graph<VertexCount>& graph, int sourceVertex)
{
//...
while (!minHeap.empty())
{
auto [fromVertex, currentDistance] = minHeap.top(); minHeap.pop();
for (const auto& [to, weight] : graph.AdjList[fromVertex])
{
int newDistance = weight + currentDistance;
if (newDistance < shortestPaths[to])
{
shortestPaths[to] = newDistance;
#ifndef NDEBUG
std::cout << std::format("Found shortest path from {} to {} with weight = {}\n", sourceVertex + 1, to + 1, newDistance);
#endif
minHeap.emplace(to, newDistance);
}
}
}
return shortestPaths;
}If we run this program - we will get the following output.
Found shortest path from 1 to 2 with weight = 7
Found shortest path from 1 to 6 with weight = 14
Found shortest path from 1 to 3 with weight = 9
Found shortest path from 1 to 4 with weight = 22
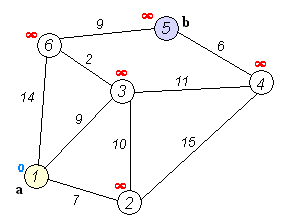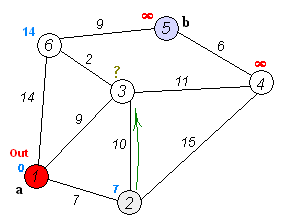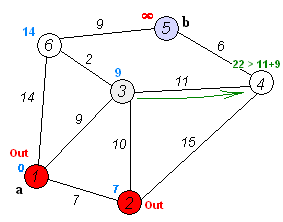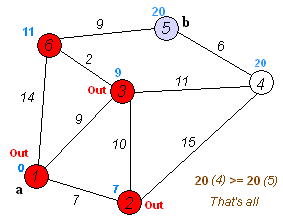
Found shortest path from 1 to 6 with weight = 11
Found shortest path from 1 to 4 with weight = 20
Found shortest path from 1 to 5 with weight = 20
Shortest paths:
1->1 = 0
1->2 = 7
1->3 = 9
1->4 = 20
1->5 = 20
1->6 = 11All code for this topic is available on Github.
[1] Wikipedia - Dijkstra’s algorithm
If you noticed an error or just want to drop me a message - reach me via LinkedIn or email.
Home