Let us port the Dijsktra’s algorithm implementation from the previous post from C++ to Rust as an exercise.
First, we define our Graph data structure. Fortunately there is support for generics.
struct Edge {
to: usize,
weight: u32,
}
struct Graph<const VERTEX_COUNT: usize> {
adj_list: [Vec<Edge>; VERTEX_COUNT],
}
impl<const VERTEX_COUNT: usize> Graph<VERTEX_COUNT> {
pub fn new() -> Self {
Self {
adj_list: array::from_fn(|_| Vec::new()),
}
}
pub fn add_edge(&mut self, from: usize, to: usize, weight: u32) {
assert!(from > 0 && from <= VERTEX_COUNT, "Cannot add edge from vertex: {}", from);
assert!(to > 0 && to <= VERTEX_COUNT, "Cannot add edge to vertex: {}", to);
let from_ix: usize = from - 1;
let to_ix: usize = to - 1;
self.adj_list[from_ix].push(Edge { to: to_ix, weight });
self.adj_list[to_ix].push(Edge { to: from_ix, weight });
}
}In contrast to C++, there is no need to declare methods separately -
you can just write method definitions in the implementation block.
Similar to Python and Golang you have to explicitely pass a mutable
reference to this, which in Rust is called
self.
One pleasant feature of the struct’s instantiation - Rust forces you
to explicitely tell to which field you are assigning a value as in the
example of Edge {to: to_ix, weight}.
As you can see this can be skipped when the names in the current scope
match.
Another interesting aspect - to initialize the adjacency list, which
is an array of vectors, we implement a new() method.
Here for each element of the array the closure
|_| Vec::new() is called to create an empty vector.
Despite it’s name the object is not constructed on the heap.
new() seems to be a convention and is conseptually a
constructor.
Let us add a helper function to print paths and fill the graph.
Here we pass the graph by reference. And it is non-mutable, as is the
default in Rust.
fn print_paths<const VERTEX_COUNT: usize>(source_vertex: usize, paths: &[u32; VERTEX_COUNT]) {
println!("Shortest paths:");
for (i, &distance) in paths.iter().enumerate() {
if distance < u32::MAX {
println!("{}->{} = {}", source_vertex, i + 1, distance);
}
}
}
fn main() {
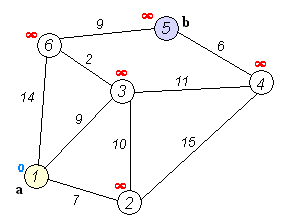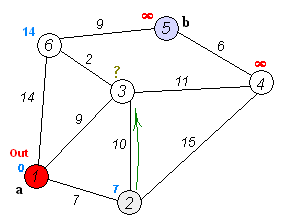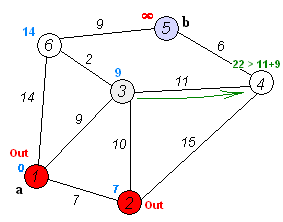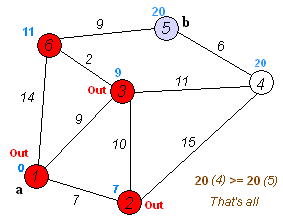
let mut graph: Graph<6> = Graph::new();
graph.add_edge(1, 2, 7);
graph.add_edge(1, 6, 14);
graph.add_edge(1, 3, 9);
graph.add_edge(2, 3, 10);
graph.add_edge(2, 4, 15);
graph.add_edge(3, 6, 2);
graph.add_edge(3, 4, 11);
graph.add_edge(4, 5, 6);
graph.add_edge(5, 6, 9);
let from: usize = 1;
let shortest_paths = find_shortest_paths(&graph, from);
print_paths(from, &shortest_paths);
}It is the same graph that we used before.

Let us implement the algorithm itself.
Here we implement a generic function accepting a graph, a source vertex and returning an array of shortest paths to each vertex in the graph.
Similarly we initialize an array of shortest paths to max integer and set the distance to the source vertex itself as 0.
fn find_shortest_paths<const VERTEX_COUNT: usize>(graph: &Graph<VERTEX_COUNT>, mut source_vertex: usize) -> [u32; VERTEX_COUNT] {
assert!(source_vertex > 0 && source_vertex <= VERTEX_COUNT, "Invalid vertex provided: {}", source_vertex);
source_vertex = source_vertex - 1; // 0-indexed
let mut shortest_paths: [u32; VERTEX_COUNT] = array::from_fn(|_| u32::MAX); // distance to all vertices is unknown
shortest_paths[source_vertex] = 0; // path to the source vertex itself it zero
// ...
}To use a minimum heap and store the current paths in the graph we
need to use the BinaryHeap data structure in Rust and
implement Ord and PartialOrd traits for the
Path structure.
#[derive(Eq, PartialEq)]
struct Path
{
to: usize,
distance: u32,
}
impl Ord for Path {
fn cmp(&self, other: &Self) -> std::cmp::Ordering {
other.distance.cmp(&self.distance) // Reverse for min-heap
}
}
impl PartialOrd for Path {
fn partial_cmp(&self, other: &Self) -> Option<std::cmp::Ordering> {
Some(self.cmp(other))
}
}By default Rust’s BinaryHeap is a max heap, so a custom PartialOrd is required for Path.
We declare that struct Path implements equality
comparisons == and != with
#[derive(Eq, PartialEq)].
The only required operation for the BinaryHeap is
PartialOrd, which just delegates to the Ord’s cmp.
Reverse comparison
(other.distance.cmp(&self.distance)) makes this a
min-heap (default is max-heap).
With this in place we can put the source vertex into the heap and run the Dijkstra’s algorithm.
fn find_shortest_paths/*...*/{
// ...
let mut min_heap: BinaryHeap<Path> = Default::default();
min_heap.push(Path{to: source_vertex, distance: 0}); // start at the source vertex
while !min_heap.is_empty() {
if let Some(Path { to: from_vertex, distance: current_distance }) = min_heap.pop() {
for Edge{to: to_vertex, weight} in &graph.adj_list[from_vertex] {
let new_distance: u32 = weight + current_distance;
if new_distance < shortest_paths[*to_vertex] {
shortest_paths[*to_vertex] = new_distance;
println!("Found shortest path from {} to {} with weight = {}", source_vertex + 1, to_vertex + 1, new_distance);
min_heap.push(Path{ to: *to_vertex, distance: new_distance });
}
}
}
}
shortest_paths
}An interesting aspect here is that the structured binding
Edge{to: to_vertex, weight} is a reference, so when we pass
to_vertex as an index into an array - we have to
dereference it with * first.
Another syntactical different to C++ - when doing structural bindings
- the default field names are used, unless an alias is specified.
Sometimes to make the algorithm more readable an alias as in
Path{tp: from_vertex, distance: current_distance} really
comes in handy.
Since Rust is an expression-based language - we can return the array
by just having the variable name as the last line of the function,
without explicit returns.
Ok, fair enough, Scala does the same.
If we run this program - we will get the following output.
Found shortest path from 1 to 2 with weight = 7
Found shortest path from 1 to 6 with weight = 14
Found shortest path from 1 to 3 with weight = 9
Found shortest path from 1 to 4 with weight = 22
Found shortest path from 1 to 6 with weight = 11
Found shortest path from 1 to 4 with weight = 20
Found shortest path from 1 to 5 with weight = 20
Shortest paths:
1->1 = 0
1->2 = 7
1->3 = 9
1->4 = 20
1->5 = 20
1->6 = 11And here we go - the same algorithm, but ported from C++ to Rust!
All code for this topic is available on Github.
If you noticed an error or just want to drop me a message - reach me via LinkedIn or email.
Home